| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 케라스 정리
- 파이토치
- 영상처리
- object detection
- 미디언 필터링
- matlab 영상처리
- pytorch zero to all
- tensorflow 예제
- 팀프로젝트
- pytorch
- c++
- 가우시안 필터링
- 딥러닝
- 딥러닝 공부
- c언어
- 파이토치 김성훈 교수님 강의 정리
- TensorFlow
- 모두의 딥러닝 예제
- 해리스 코너 검출
- C언어 공부
- c언어 정리
- c++공부
- MFC 프로그래밍
- 딥러닝 스터디
- 골빈해커
- 김성훈 교수님 PyTorch
- 모두의 딥러닝
- Pytorch Lecture
- 파이토치 강의 정리
- 컴퓨터 비전
- Today
- Total
ComputerVision Jack
PyTorch Lecture 07 : Wide and Deep 본문
이번 장에선 전 시간에 배운 logistic regression 네트워크를 깊고 넓게 구성하는 방법에 대해 설명해주셨습니다.
우선 설명해주신 예제로 풀어보겠습니다.
HKUST PHD Program Application
| GPA(a) | Admission? |
| 2.1 | 0 |
| 4.2 | 1 |
| 3.1 | 0 |
| 3.3 | 1 |
만약 데이터가 이런식으로 제공되어 있다면 우리가 알고있는 logistic regression으로 처리하면 됩니다.
GPA (입력) -> Linear -> Sigmoid -> y^ 식으로 접근이 가능합니다.
How about experience and other
| GPA(a) | Experience(b) | Admission? |
| 2.1 | 0.1 | 0 |
| 4.2 | 0.8 | 1 |
| 3.1 | 0.9 | 0 |
| 3.3 | 0.2 | 1 |
해당 데이터에 대해 Experience 변수가 추가된다면 어떻게 해야할까요?
GPA (입력) -> Linear -> sigmoid -> y^
Experience(입력)
이런식으로 식을 짜야합니다.
Matrix Multiplication
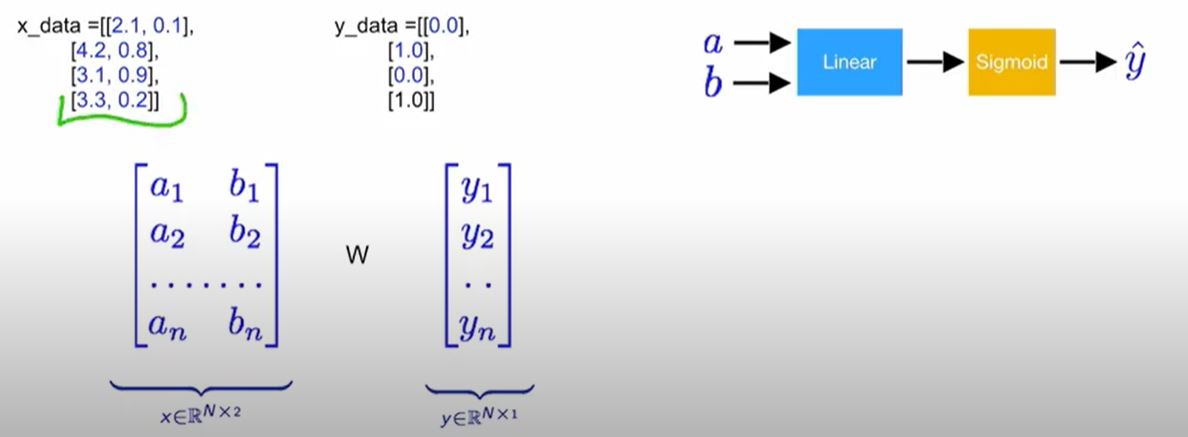
이렇게 다변수에 대해 y^을 처리해야 할 경우가 발생하기 때문에 행렬이라는 개념이 도입되고, 행렬의 곱 연산을 통해 진행할 수 있습니다. 즉 코드적인 부분으로 접근한다면
linear = torch.nn.Linear(2, 1)
y_pred = linear(x_data)로 접근이 가능합니다. 입력 2개의 값에 대해 결과값 1로 매칭되는 것을 확인할 수 있습니다.
Go Deep!

또한 해당 데이터셋에 대해 layer를 추가하여 네트워크를 deep하게 꾸려갈 수도 있습니다.
해당 내용에 대해선 코드를 다룰 때 좀더 알아보겠습니다.
Classifying Diabetes
이번 예제는 데이터를 직접 저희가 입력하는 것이 아닌 csv 파일을 읽어와서 처리하는 방식입니다.
제공된 데이터 셋은 당뇨에 관련된 데이터 셋이며 우선 데이터셋을 확인해보겠습니다.
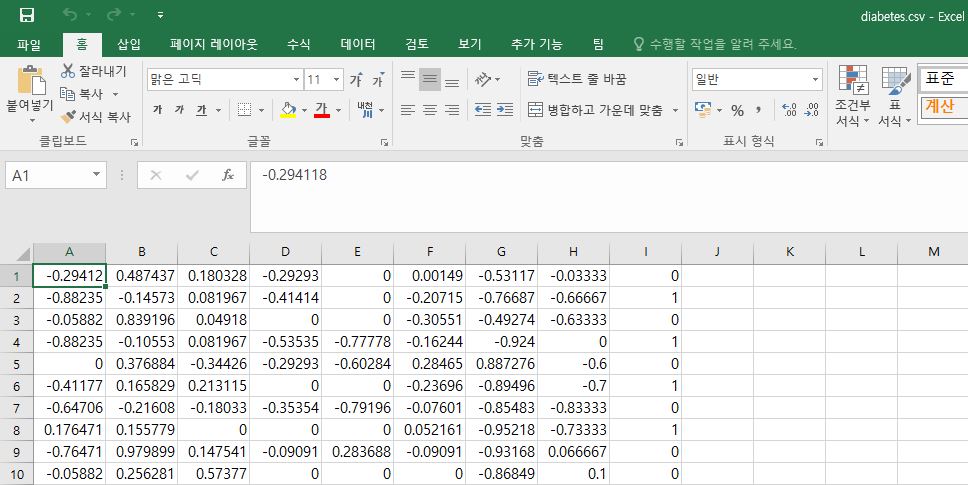
엑셀 파일로 접근해서 본다면 A열부터 H열까진 x 데이터에 해당하고, I열은 x 데이터를 토대로 추출된 y 데이터 값 입니다. 따라서 shape을 살펴보면 x_data는 (n, 8) 이고, y_data는 (n, 1)입니다.
즉 해당 행렬 데이터로 linear에 접근한다면 x_data와 곱해지는 w는 (8, 1)로 되어야 행렬 곱셈 연산을 통해 y_data가 추출됩니다.
[07.diabets_logistic.py]
from google.colab import files
uploaded = files.upload()
#우선 코렙에서 해당 코드를 통해 데이터 파일을 작업환경으로 가져옵니다.
from torch import nn, optim, from_numpy
import numpy as np
# 파이토치 라이브러리와 해당 csv파일을 다루기 위한 수치해석 라이브러리 numpy를 import합니다.
xy = np.loadtxt('diabetes.csv.gz', delimiter = ',', dtype = np.float32)
x_data = from_numpy(xy[:, 0:-1])
y_data = from_numpy(xy[:, [-1]])
print(f'X\'s shape : {x_data.shape} | Y\'s shape : {y_data.shape}')
#loadtxt 함수를 사용하여 데이터를 읽어옵니다. 또한 , 구분자를 통해 데이터를 구분하며 float32 타입으로 가져옵니다.
그 다음 슬라이싱을 통해 데이터를 x, y에 분리하여 대입합니다.
class Model(nn.Module):
def __init__(self):
super(Model, self).__init__()
self.l1 = nn.Linear(8, 6)
self.l2 = nn.Linear(6, 4)
self.l3 = nn.Linear(4, 1)
self.sigmoid = nnSigmoid()
def forward(self, x):
out1 = self.sigmoid(self.l1(x))
out2 = self.sigmoid(self.l2(out1))
y_pred = self.sigmoid(self.l3(out2))
return y_pred
#해당 생성자 부분을 보시면 Linear layer를 3개의 층으로 사용해 네트워크를 깊게 형성하신 것을 볼 수 있습니다.
여기서 주의할 점은 초기 입력으로 들어가는 부분과 마지막으로 출력되는 부분에 대한 shape을 데이터와 맞춰줘야 합니다. x_data가 (n, 8)이기 때문에 초기 8을 입력으로 받아야합니다. 다음 마지막 층에선 y_data가 (n, 1)이기 때문에 몇개의 특징이 들어오건 결과는 1로 출력을 내야합니다.
해당 조건을 지킨다면 레이어 깊이 구성과 그 외의 값은 개발자의 마음대로 정할 수 있습니다.
model = Model()
# 모델 객체 생성
criterion = nn.BCELoss(reduction = 'mean')
optimizer = optim.SGD(model.parameters(), lr =0.1)
# 손실 함수와 최적화 부분에 대한 구현을 진행합니다.
for epoch in range(100):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(f'Epoch : {epoch + 1} / 100 | Loss : {loss.item():.4f}')
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 전에 배운대로 학습을 진행시켜주면 학습이 완료됩니다.
'DeepLearning > Pytorch_ZeroToAll' 카테고리의 다른 글
| PyTorch Lecture 09 : softmax Classifier (0) | 2020.10.23 |
|---|---|
| PyTorch Lecture 08 : DataLoader (0) | 2020.10.21 |
| PyTorch Lecture 06 : Logistic Regression (0) | 2020.10.12 |
| PyTorch Lecture 05 : Linear Regression in the PyTorch way (0) | 2020.10.07 |
| PyTorch Lecture 04 : Back-propagation and Autograd (0) | 2020.10.06 |




